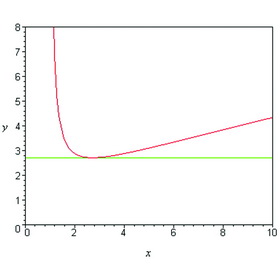函数\(f(x)=x/\ln x\)的图像

数学有三种基本运算：加法运算（包括减法运算）、乘法运算（包括除法运算）和幂运算。加法运算和乘法运算都有交换律，即对两个数\(a\)和\(b\)，\(a+b=b+a\)，\(ab=ba\)。但是幂运算却没有类似的交换律，一般说来\(a^b≠b^a\)。比如\(2^3<3^2\)，而\(3^4>4^3\)，等等。那么，\(a^b\)和\(b^a\)的大小有怎样的关系呢？比如，对数学中最重要的两个常数\(\pi\)和\(e\)，\(e^\pi\)和\(\pi^e\)到底哪个大呢？这是一个比较有趣的问题。由于\(\pi\)和\(e\)都是超越数，\(e^\pi\)和\(\pi^e\)不是一下就能算出来的，通过计算它们的数值来比较它们的大小也不是一个有价值的办法。

我们考虑一般的问题：假设\(a>b>1\)，如何比较\(a^b\)和\(b^a\)的大小。这样的幂运算是比较复杂的，我们可以考虑它们的对数，将幂运算化为乘法运算，即比较\(b\ln a\)和\(a\ln b\)的大小，这里\(\ln a\)表示\(a\)的自然对数。这两个数中都是既有\(a\)又有\(b\)，再转化一下，只要比较\(a\ln a\)和\(b\ln b\)的大小就可。现在，问题就变成研究函数\(f(x)=x/\ln x(x>1)\)，当变量\(x\)取不同值时，其函数值的大小变化。也就是说将问题转化成研究函数\(f(x)\)的性质，比如单调性、最大（小）值等。如果\(f(x)\)单调增，则当\(a>b\)时就有\(f(a)>f(b)\)。

这个函数\(f(x)=x/\ln x\)还是比较复杂的，单凭初等数学的知识要弄清这个函数的性质有点困难。尽管如此，我们还是可以做些初步的观察。

比如，让\(x\)逐渐变小趋近于1，则分母\(\ln x\)会越来越小，且趋近于0。因此函数值\(f(x)=x/\ln x\)会越来越大，且趋向于无穷大。而当\(x\)逐渐变大并趋于无穷大，情况就稍微复杂一些。记\(k=\ln x\)，则\(f(x)=x/\ln x=e^k/k\)。我们知道，\(x\)趋向于无穷大意味着\(k\)也趋向于无穷大。由于\(e>2\)，而我们又知道\(2^k\)的增长速度要远远快于\(k\)自身的增长，于是，可以看出\(f(x)=x/\ln x=e^k/k\)也会随着\(x\)的增大而越来越大，直至趋于无穷大。现在，我们对这个函数可以有个大概的感觉了：它的图像应该在1和∞两端上翘，并延伸至无穷大。如此说来，函数\(f(x)\)应该在区间(1，∞)中间有一个最小值（如图）。那么，这个最小值在哪里出现呢？初等数学对此无能为力了，需要利用大学数学中的微积分知识。直观上看，图像曲线在最小值处应有水平的切线，而判断切线是否水平，这是微积分轻而易举就能做到的。函数\(f(x)=x/\ln x\)，当且仅当\(x\)满足\(\ln x–1=0\)时才有水平切线。于是，我们知道，\(f(x)\)在\(x=e\)处的取值是最小的，只要\(x≠e\)，一定有\(f(x)=x/\ln x>f(e)=e/\ln e\)，或者\(x\ln e>e\ln x\)，回到指数形式，就有\(e^x>x^e\)。而\(\pi≠e\)，我们自然就有\(e^\pi>\pi^e\)。

这个例子告诉我们，初等数学能够解决的问题其实是非常有限的。如果要解决比较复杂的问题，还需要学习更多的数学知识。而随着现代科技的发展，需要用到的数学知识将会越来越广泛。

初等数学能够解决的问题是有限的，证明 需要到高等数学知识